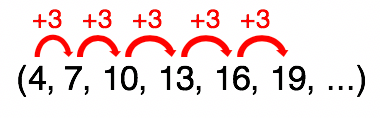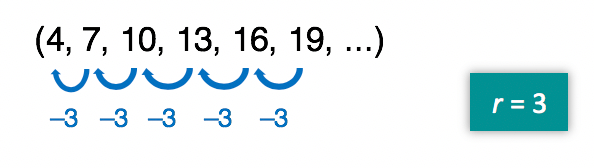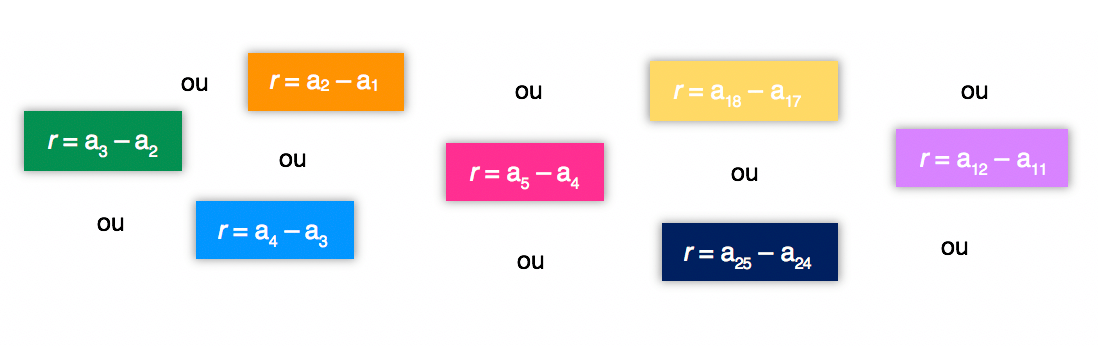Olá Pessoal!!!
Tudo bem com vocês?
Hoje iremos apreender um pouquinho mais, então preparem o caderno,
lápis e borracha, deixem tudo pertinho de vocês para que possam anotar tudinho
assim ficará bem mais fácil de apreender o assunto de hoje.
Bora lá?
O QUE É UMA PROGRESSÃO ARITMÉTICA?
Como foi dito logo no início do texto, uma PA é uma sequência em que cada termo, a partir do segundo, é igual a soma do anterior com uma constante r dada. Para que a ideia fique mais clara, vamos analisar a seguinte sequência:
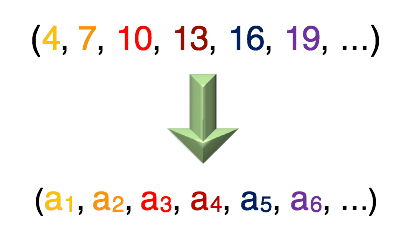
(4, 7, 10, 13, 16, 19, …)
Observem que a sequência acima é formada pelos números 4, 7, 10, 13, 16, 19, e por outros que seguem rumo ao mais infinito. Estes números são os chamados termos da progressão. Pela ordem em que são apresentados, é que definimos qual é o primeiro termo (a1), o segundo termo (a2), o terceiro termo (a3) e assim sucessivamente.
Mas o mais importante de tudo, é repararmos que existe uma certa relação constante do a1 para o a2, do a2 para o a3, do a3 para o a4, do a4 para o a5, do a5 para o a6, e que segue infinitamente. Podemos dizer que cada termo, a partir de a2, é obtido da soma do anterior a um número fixo. Sendo assim, qual é o número que somado a 4 resulta em 7? Qual é o número que somado a 7 resulta em 10? Ou ainda, qual é o número que somado a 10 resulta em 13? Sempre 3!
Incrível, não é mesmo? Este número fixo, que somado a cada um dos termos antecedentes dá origem a cada um dos termos sucessores da sequência, e que no nosso exemplo vale 3, não é ninguém menos do que a razão da progressão aritmética (r )!
QUAL É A FÓRMULA DA RAZÃO DE UMA PA?
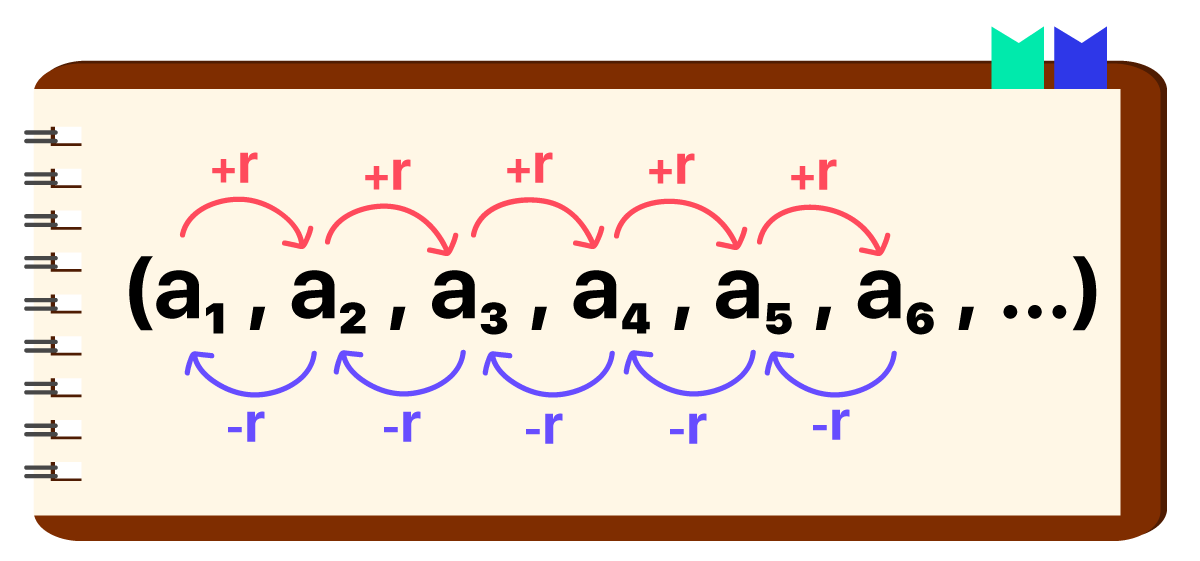
Sob um segundo ponto de vista, também podemos dizer que uma PA é uma sequência em que cada termo, a partir do penúltimo, é igual a diferença entre seu sucessor e uma constante r dada. Por isso, se descontarmos de qualquer um dos termos do nosso exemplo (com exceção do a1) o valor 3, encontraremos seu termo antecessor.
Essa ideia nos permite definir uma fórmula para a razão r da PA. Olhem só!
É, parece que fui um pouco modesto ao afirmar que encontraríamos apenas uma fórmula da razão da PA. O fato é que podemos obter a razão desta progressão descontando de qualquer um de seus termos (sempre com exceção do a1), o termo antecedente. Podemos utilizar os valores do primeiro e do segundo termo, do quarto e do quinto, e até do vigésimo quarto e do vigésimo quinto, se eles existirem e conhecermos seus valores. Tudo é válido, desde que a razão seja mantida por toda a sequência.
Entendido? Então vamos a alguns exemplos para que não restem dúvidas!
EXEMPLOS RESOLVIDOS SOBRE A PROGRESSÃO ARITMÉTICA
Dadas as sequências abaixo, verifique se são progressões aritméticas.
a. (1, 3, 5, 7, 9, …)
Vocês devem estar curiosos para saber por que tenho descrito cada uma das sequências que estudamos em meio a parênteses. Pois então, os parênteses são utilizados para indicar que os números ou termos da sequência estão seguindo uma ordem. Bom, parece mesmo haver uma relação constante entre os valores da sequência do item a. Mas para que possamos ter certeza de que se trata de uma PA, faremos o cálculo de sua razão r.
r = a2 – a1 = a3 – a2 = a4 – a3
r = 3 – 1 = 5 – 3 = 7 – 5
r = 2 = 2 = 2
r = 2
Vejam que fizemos vários cálculos a fim de determinar a razão r da sequência. Em todos eles, alcançamos o mesmo resultado, o valor 2. Por esse motivo, não há dúvidas de que se trata de uma PA! Veremos agora, como as próximas sequências irão se comportar.
b. (2, 4, 8, 16, 32, …)
Hum, visualmente parece que nessa sequência também existe uma relação constante entre os termos. Para averiguarmos se é mesmo uma PA, vamos realizar o cálculo da sua razão r.
r = a2 – a1 = a3 – a2 = a4 – a3
r = 4 – 2 = 8 – 4 = 16 – 8
2 ≠ 4 ≠ 8
Opa! Apesar de parecer que havia uma relação constante entre os termos da sequência, eles não se relacionam conforme uma progressão aritmética. Isso fica evidente quando calculamos a razão entre diversos termos, sem que os resultados coincidam. Se vocês estiverem curiosos para saber que tipo de sequência é essa, basta clicar aqui.
Quando a razão da PA não é positiva
c. (0, –2, –4, –6, –8, …)
Muito embora a sequência apresentada neste item seja formada por números negativos, podemos observar que também existe uma certa relação constante entre seus termos. É hora de realizarmos o cálculo da razão r.
r = a2 – a1= a3 – a2 = a4 – a3
r = –2 – 0 = –4 – (–2) = –6 – (–4)
r = – 2 = – 2 = – 2
r = –2
A partir deste cálculo, podemos concluir que a sequência (0, –2, –4, –6, –8, …) é uma PA de razão igual a –2.
d. (3, 3, 3, 3, 3, 3, …)
E aí, o que acharam da sequência acima? Parece estranho que uma PA seja uma sequência de números repetidos, não é mesmo? Mas antes de tirarmos conclusões precipitadas, vamos seguir nosso procedimento calculando a razão r:
r = a2 – a1= a3 – a2 = a4 – a3
r = 3 – 3 = 3 – 3 = 3 – 3
r = 0 = 0 = 0
r = 0
Se todos os cálculos da razão resultaram no mesmo valor, podemos sim afirmar que a sequência (3, 3, 3, 3, 3, 3, …) é uma progressão aritmética de razão igual a 0.
É, pessoal, dentro dos exemplos que resolvemos, descobrimos que 3 sequências, das 4 apresentadas, formavam uma PA. Além disso, notamos que cada uma das progressões encontradas possuía uma razão diferente, positiva, negativa ou mesmo igual a zero. Parece um detalhe insignificante, mas vocês verão a seguir que o valor da razão de cada progressão aritmética determina sua classificação dentro de 3 categorias. Vem comigo!
CLASSIFICAÇÃO DE UMA PROGRESSÃO ARITMÉTICA
É muito simples classificar uma PA, pessoal! Basta ficar de olho no valor da razão r, e no comportamento da sequência ao longo dos termos. Olhem só!
PA Crescente
Uma PA é crescente quando sua razão é positiva, ou seja, quando r > 0. Desta forma, cada termo seguinte é sempre maior que o anterior, isto é, os valores dos termos sempre irão aumentar, crescer.
(6, 10, 14, 18, …)
A sequência acima é uma PA crescente. Se ficarmos atentos ao valor de seus termos, veremos que eles estão sempre crescendo, e que a razão da progressão é positiva, r = 4.
PA Decrescente
Uma PA é decrescente quando sua razão é negativa, ou seja, r < 0. Assim, cada termo seguinte é sempre menor que o anterior, isto é, os valores dos termos sempre irão diminuir, decrescer.
(13, 8, 3, –2, –7, …)
A sequência acima é uma PA decrescente, pois sua razão é negativa, r = –5. Reparando com atenção nos termos da sequência, é possível perceber que seus valores estão diminuindo, decrescendo.
PA Constante
Uma PA é constante ou estacionária, quando sua razão é nula, ou seja, r = 0. Neste caso, todos os termos da sequência são iguais, isto é, não se alteram.
(5, 5, 5, 5, …)
A sequência (5, 5, 5, 5, …) é uma PA constante. Seus termos nunca se alteram, e, portanto, sua razão r é igual a zero.
Interessante, não é, pessoal? A verdade é que tudo que acabamos de estudar é apenas uma pequena parte de todo o conhecimento que envolve as progressões aritméticas. Por isso, fiquem atentos a todos os posts do blog sobre o assunto, e não deixem de ver o vídeo que deixo em anexo . Nele, vocês conseguem revisar tudo o que aprendemos hoje!
Progressão Aritmética Vídeo 01, 02 e 03 assistam na ordem.